Sine matrix

The sine matrix [1] captures features of interacting atoms in a periodic system with a very low computational cost. The matrix elements are defined by

\[\begin{split}\begin{equation} M_{ij}^\mathrm{sine}=\left\{ \begin{matrix} 0.5 Z_i^{2.4} & \text{for } i = j \\ \frac{Z_i Z_j}{\lvert \mathbf{B} \cdot \sum_{k=\{x,y,z\}} \hat{\mathbf{e}}_k \sin^2 \left( \pi \mathbf{B}^{-1} \cdot \left( \mathbf{R}_{i} - \mathbf{R}_{j} \right) \right)\rvert} & \text{for } i \neq j \end{matrix} \right. \end{equation}\end{split}\]

Here \(\mathbf{B}\) is a matrix formed by the lattice vectors and \(\hat{\mathbf{e}}_k\) are the cartesian unit vectors. This functional form has no physical interpretation, but it captures some of the properties of the Coulomb interaction, such as the periodicity of the crystal lattice and an infinite energy when two atoms overlap.

Setup

Instantiating the object that is used to create Sine matrices can be done as follows:

from dscribe.descriptors import SineMatrix

# Setting up the sine matrix descriptor
sm = SineMatrix(
    n_atoms_max=6,
    permutation="sorted_l2",
    sparse=False,
    flatten=True
)

The constructor takes the following parameters:

Creation

After the Sine matrix has been set up, it may be used on periodic atomic structures with the create()-method.

from ase.build import bulk

# NaCl crystal created as an ASE.Atoms
nacl = bulk("NaCl", "rocksalt", a=5.64)

# Create output for the system
nacl_sine = sm.create(nacl)

# Create output for multiple system
al = bulk("Al", "fcc", a=4.046)
fe = bulk("Fe", "bcc", a=2.856)
samples = [nacl, al, fe]
sine_matrices = sm.create(samples)            # Serial
sine_matrices = sm.create(samples, n_jobs=2)  # Parallel

The call syntax for the create-function is as follows:

Note that if you specify in n_atoms_max a lower number than atoms in your structure it will cause an error. The output will in this case be a flattened matrix, specifically a numpy array with size #atoms * #atoms. The number of features may be requested beforehand with the get_number_of_features()-method.

In the case of multiple samples, the creation can also be parallellized by using the n_jobs-parameter. This splits the list of structures into equally sized parts and spaws a separate process to handle each part.

Examples

The following examples demonstrate usage of the descriptor. These examples are also available in dscribe/examples/sinematrix.py.

Interaction in a periodic crystal

The following code calculates the interaction value, as defined by the sine matrix, between two aluminum atoms in an FCC-lattice. The values are calculated in the xy-plane.

import numpy as np
from ase import Atoms
import matplotlib.pyplot as mpl
from mpl_toolkits.axes_grid1 import make_axes_locatable

# FCC aluminum crystal
system = bulk("Al", "fcc", cubic=False)

# Calculate the sine matrix entries for a 2D slice at z=0
sm = SineMatrix(
    n_atoms_max=2,
    permutation="none",
    sparse=False,
    flatten=False
)
n = 100
d = 10
grid = np.zeros((n, n))
values = np.linspace(0, d, n)
for ix, x in enumerate(values):
    for iy, y in enumerate(values):
        i_atom = Atoms(["Al"], positions=[[x, y, 0]])
        i_sys = system.copy()+i_atom
        i_sm = sm.create(i_sys)
        i_sm = i_sm[0, 1]
        grid[ix, iy] = i_sm

# Plot the resulting sine matrix values
maxval = 150
fig, ax = mpl.subplots(figsize=(6, 5))
np.clip(grid, a_min=None, a_max=maxval, out=grid)
c1 = ax.contourf(values, values, grid, levels=500)
ax.contour(values, values, grid, levels=5, colors="k", linewidths=0.5, alpha=0.5)
the_divider = make_axes_locatable(ax)
color_axis = the_divider.append_axes("right", size="5%", pad=0.2)
cbar = fig.colorbar(c1, cax=color_axis, ticks=[grid.min(), grid.max()])
ax.axis('equal')
ax.set_ylabel("y (Å)")
ax.set_xlabel("x (Å)")
mpl.tight_layout()
mpl.show()

This code will result in the following plot:

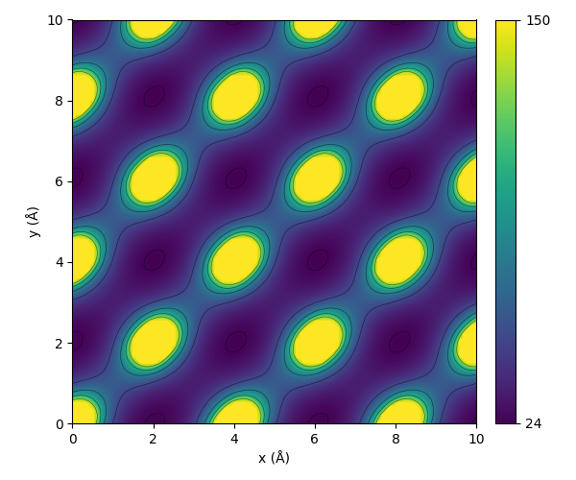
Illustration of the periodic interaction defined by the sine matrix.

From the figure one can see that the sine matrix correctly encodes the periodicity of the lattice. Notice that the shape of the interaction is however not perfectly spherical.

1: Felix Faber, Alexander Lindmaa, O. Anatole von Lilienfeld, and Rickard Armiento. Crystal structure representations for machine learning models of formation energies. International Journal of Quantum Chemistry, 115(16):1094–1101, 8 2015. doi:10.1002/qua.24917.