Many-body Tensor Representation

The many-body tensor representation (MBTR) [1] encodes a structure by using a distribution of different structural motifs. It can be used directly for both finite and periodic systems. MBTR is especially suitable for applications where interpretability of the input is important because the features can be easily visualized and they correspond to specific structural properties of the system.

In MBTR a geometry function \(g_k\) is used to transform a chain of \(k\) atoms, into a single scalar value. The distribution of these scalar values is then constructed with kernel density estimation to represent the structure.

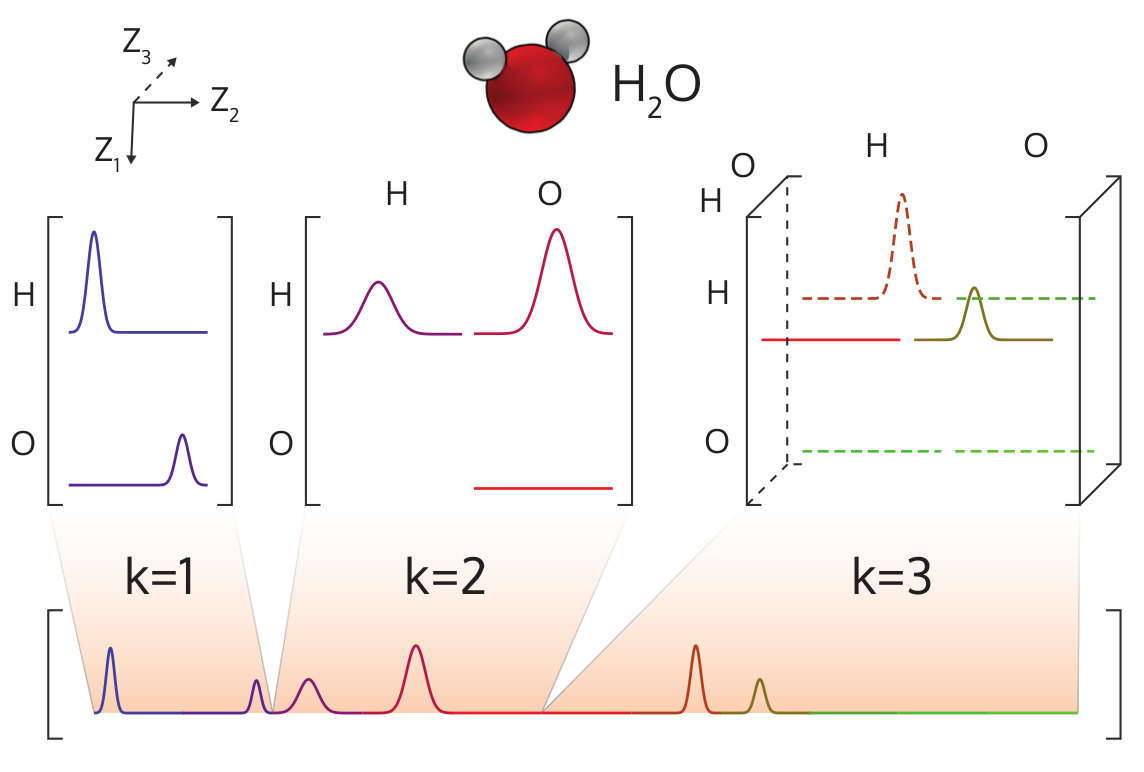
MBTR stratification — Illustration of the MBTR output for a water molecule.

Setup

Instantiating an MBTR descriptor can be done as follows:

from dscribe.descriptors import MBTR

# Setup
mbtr = MBTR(
    species=["H", "O"],
    geometry={"function": "inverse_distance"},
    grid={"min": 0, "max": 1, "n": 100, "sigma": 0.1},
    weighting={"function": "exp", "scale": 0.5, "threshold": 1e-3},
    periodic=False,
    normalization="l2",
)

The arguments have the following effect:

MBTR.__init__(geometry=None, grid=None, weighting=None, normalize_gaussians=True, normalization='none', species=None, periodic=False, sparse=False, dtype='float64')[source]

Parameters:

geometry (dict) –
Setup the geometry function. For example:
```
"geometry": {"function": "atomic_number"}
```
The geometry function determines the degree \(k\) for MBTR. The order \(k\) tells how many atoms are involved in the calculation and thus also heavily influence the computational time.

The following geometry functions are available:
- \(k=1\)
  - "atomic_number": The atomic number.
- \(k=2\)
  - "distance": Pairwise distance in angstroms.
  - "inverse_distance": Pairwise inverse distance in 1/angstrom.
- \(k=3\)
  - "angle": Angle in degrees.
  - "cosine": Cosine of the angle.
grid (dict) –
Setup the discretization grid. For example:
```
"grid": {"min": 0.1, "max": 2, "sigma": 0.1, "n": 50}
```
In the grid setup min is the minimum value of the axis, max is the maximum value of the axis, sigma is the standard deviation of the gaussian broadening and n is the number of points sampled on the grid.
weighting (dict) –
Setup the weighting function and its parameters. For example:
```
"weighting" : {"function": "exp", "r_cut": 10, "threshold": 1e-3}
```
The following weighting functions are available:
- \(k=1\)
  - "unity": No weighting.
- \(k=2\)
  - "unity": No weighting.
  - "exp": Weighting of the form \(e^{-sx}\)
  - "inverse_square": Weighting of the form \(1/(x^2)\)
- \(k=3\)
  - "unity": No weighting.
  - "exp": Weighting of the form \(e^{-sx}\)
  - "smooth_cutoff": Weighting of the form \(f_{ij}f_{ik}\),
    where \(f = 1+y(x/r_{cut})^{y+1}-(y+1)(x/r_{cut})^{y}\)
The meaning of \(x\) changes for different terms as follows:
- For \(k=2\): \(x\) = Distance between A->B
- For \(k=3\): \(x\) = Distance from A->B->C->A.
The exponential weighting is motivated by the exponential decay of screened Coulombic interactions in solids. In the exponential weighting the parameters threshold determines the value of the weighting function after which the rest of the terms will be ignored. Either the parameter scale or r_cut can be used to determine the parameter \(s\): scale directly corresponds to this value whereas r_cut can be used to indirectly determine it through \(s=-\log()\):.

The inverse square and smooth cutoff function weightings use a cutoff parameter r_cut, which is a radial distance after which the rest of the atoms will be ignored. For the smooth cutoff function, additional weighting key sharpness can be added, which changes the value of \(y\). If a value for it is not provided, it defaults to 2.
normalize_gaussians (bool) – Determines whether the gaussians are normalized to an area of 1. Defaults to True. If False, the normalization factor is dropped and the gaussians have the form. \(e^{-(x-\mu)^2/2\sigma^2}\)
normalization (str) –
Determines the method for normalizing the output. The available options are:
- "none": No normalization.
- "l2": Normalize the Euclidean length of the output to unity.
- "n_atoms": Normalize the output by dividing it with the number of atoms in the system. If the system is periodic, the number of atoms is determined from the given unit cell.
- "valle_oganov": Use Valle-Oganov descriptor normalization, with system cell volume and numbers of different atoms in the cell.
species (iterable) – The chemical species as a list of atomic numbers or as a list of chemical symbols. Notice that this is not the atomic numbers that are present for an individual system, but should contain all the elements that are ever going to be encountered when creating the descriptors for a set of systems. Keeping the number of chemical speices as low as possible is preferable.
periodic (bool) – Set to true if you want the descriptor output to respect the periodicity of the atomic systems (see the pbc-parameter in the constructor of ase.Atoms).
sparse (bool) – Whether the output should be a sparse matrix or a dense numpy array.
dtype (str) –
The data type of the output. Valid options are:
- "float32": Single precision floating point numbers.
- "float64": Double precision floating point numbers.

Most noteworthy is that the geometry function determines the degree \(k\) of MBTR. This degree directly determines how many atoms need to be taken into account when calculating the MBTR values (e.g. \(k=2\) means that each pair of atoms contributes to MBTR). Here is a brief summary of the currently supported geometry functions and their weighting functions for each degree \(k\):

The geometry and weighting functions
	Geometry functions	Weighting functions
\(k=1\)	`"atomic_number"`: The atomic numbers.	`"unity"`: No weighting.
\(k=2\)	`"distance"`: Pairwise distance in angstroms. `"inverse_distance"`: Pairwise inverse distance in 1/angstrom.	`"unity"`: No weighting. `"exp"`: Weighting of the form \(e^{-sx}\), where x is the distance between the two atoms. `"inverse_square"`: Weighting of the form \(1/(x^2)\), where x is the distance between the two atoms.
\(k=3\)	`"angle"`: Angle in degrees. `"cosine"`: Cosine of the angle.	`"unity"`: No weighting. `"exp"`: Weighting of the form \(e^{-sx}\), where x is the perimeter of the triangle formed by the tree atoms. `"smooth_cutoff"`: Weighting of the form \(f_{ij}f_{ik}\) defined by \(f = 1+y(x/r_{cutoff})^{y+1}-(y+1)(x/r_{cutoff})^{y}\), where x is the distance between two atoms, \(r_{cutoff}\) is the radial cutoff distance and y is a sharpness parameter which defaults to 2.

Creation

After MBTR has been set up, it may be used on atomic structures with the create()-method.

from ase.build import molecule

water = molecule("H2O")

# Create MBTR output for the system
mbtr_water = mbtr.create(water)

print(mbtr_water)
print(mbtr_water.shape)

The call syntax for the create-function is as follows:

MBTR.create(system, n_jobs=1, only_physical_cores=False, verbose=False)[source]

Return MBTR output for the given systems.

Parameters:

system (ase.Atoms or list of ase.Atoms) – One or many atomic structures.
n_jobs (int) – Number of parallel jobs to instantiate. Parallellizes the calculation across samples. Defaults to serial calculation with n_jobs=1. If a negative number is given, the used cpus will be calculated with, n_cpus + n_jobs, where n_cpus is the amount of CPUs as reported by the OS. With only_physical_cores you can control which types of CPUs are counted in n_cpus.
only_physical_cores (bool) – If a negative n_jobs is given, determines which types of CPUs are used in calculating the number of jobs. If set to False (default), also virtual CPUs are counted. If set to True, only physical CPUs are counted.
verbose (bool) – Controls whether to print the progress of each job into to the console.

Returns:

MBTR for the given systems. The return type depends on the ‘sparse’ attribute.

Return type:

np.ndarray | sparse.COO

The output will in this case be a numpy array with shape [n_positions, n_features]. The number of features may be requested beforehand with the get_number_of_features()-method.

Examples

The following examples demonstrate common use cases for the descriptor. These examples are also available in dscribe/examples/mbtr.py.

Locating information

If the MBTR setup has been specified with flatten=True, the output is flattened into a single vector and it can become difficult to identify which parts correspond to which element combinations. To overcome this, the MBTR class provides the get_location()-method. This method can be used to query for the slice that contains a specific element combination. The following example demonstrates its usage.

# The locations of specific element combinations can be retrieved like this.
ho_loc = mbtr.get_location(("H", "O"))

# These locations can be directly used to slice the corresponding part from an
# MBTR output for e.g. plotting.
mbtr_water[ho_loc]

Visualization

The MBTR output vector can be visualized easily. The following snippet demonstrates how the output for \(k=2\) can be visualized with matplotlib.

from ase.build import bulk
import matplotlib.pyplot as mpl

nacl = bulk("NaCl", "rocksalt", a=5.64)
decay = 0.5
mbtr = MBTR(
    species=["Na", "Cl"],
    geometry={"function": "inverse_distance"},
    grid={"min": 0, "max": 0.5, "sigma": 0.01, "n": 200},
    weighting={"function": "exp", "scale": decay, "threshold": 1e-3},
    periodic=True,
    sparse=False
)
mbtr_output = mbtr.create(nacl)

# Create the mapping between an index in the output and the corresponding
# chemical symbol
n_elements = len(mbtr.species)
x = np.linspace(0, 0.5, 200)

# Plot k=2
fig, ax = mpl.subplots()
for i in range(n_elements):
    for j in range(n_elements):
        if j >= i:
            i_species = mbtr.species[i]
            j_species = mbtr.species[j]
            loc = mbtr.get_location((i_species, j_species))
            mpl.plot(x, mbtr_output[loc], label="{}-{}".format(i_species, j_species))
ax.set_xlabel("Inverse distance (1/angstrom)")
ax.legend()
mpl.show()

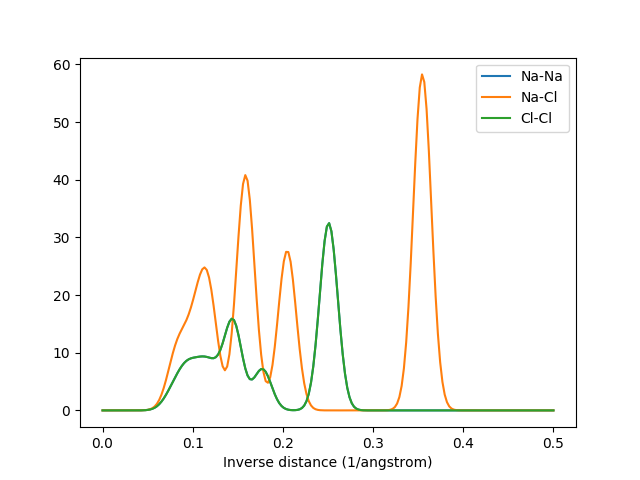
MBTR k=2 — The MBTR output for k=2. The graphs for Na-Na and Cl-Cl overlap due to their identical arrangement in the crystal.

Finite systems

For finite systems we have to specify periodic=False in the constructor. Finite systems can not have Valle-Oganov normalization, and an exception is raised if that is given. The need to apply weighting depends on the size of the system: for small systems, such as small molecules, the benefits are small. However for larger systems, such as clusters and bigger molecules, adding weighting will help in removing “noise” coming from atom combinations that are physically very far apart and do not have any meaningful direct interaction in the system. The following code demonstrates both approaches.

desc = MBTR(
    species=["C"],
    geometry={"function": "distance"},
    grid={"min": 0.4, "max": 8, "sigma": 0.1, "n": 200},
    periodic=False,
    sparse=False,
    normalization="l2",
)

system = molecule("C60")

# No weighting
output_no_weight = desc.create(system)

# Exponential weighting
desc.weighting = {"function": "exp", "scale": 1.1, "threshold": 1e-2}
output_weight = desc.create(system)

fig, ax = mpl.subplots()
x = np.linspace(0.3, 10, 200)
ax.set_xlabel("Distance angstrom")
ax.plot(x, output_no_weight, label="No weighting")
ax.plot(x, output_weight, label="Exponential weighting")
ax.legend()
mpl.show()

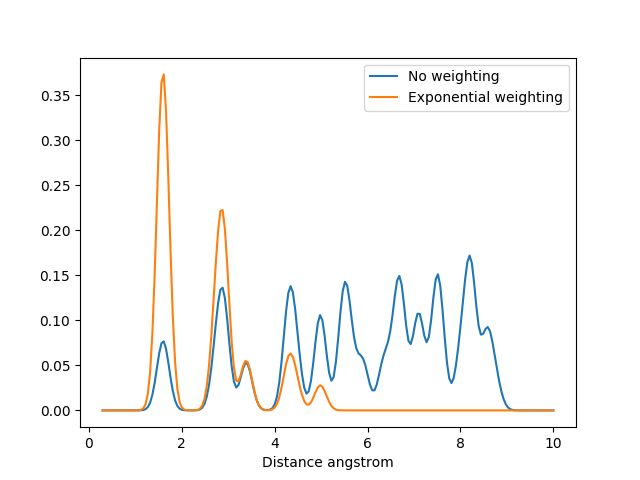
MBTR weighting — The MBTR output for C60 without weighting and with exponential weighting for \(k=2\). Without the weighting the carbon pairs that are far away will have the highest intensity and dominate the output.

Normalization

Depending on the application, the preprocessing of the MBTR vector before feeding it into a machine learing model may be beneficial. Normalization is one of the methods that can be used to preprocess the output. Here we go through some examples of what kind of normalization can be used together with MBTR, but ultimately the need for preprocessing depends on both the predicted property and the machine learning algorithm.

The different normalization options provided in the MBTR constructor are:

“none”: No normalization is applied. If the predicted quantity is extensive - scales with the system size - and there is no need to weight the importance of the different \(k\)-terms, then no normalization should be performed.

“l2”: Output is scaled to unit Euclidean norm. This option can be used if the predicted quantity is intensive - does not scale with the system size, and if the learning method uses the Euclidean norm to determine the similarity of inputs.

“n_atoms”: The whole output is divided by the number of atoms in the system. If the system is periodic, the number of atoms is determined from the given system cell. This form of normalization does also make the output for different crystal supercells equal, but does not equalize the norm of different k-terms.

“valle_oganov”: Normalization of Valle-Oganov descriptor is applied. Each pair in \(k=2\) is multiplied by \(V/4\pi N_{A}N_{B}\), where V is the volume of the current system and \(N_{A}\) and \(N_{B}\) are the numbers of each of the pair’s elements in the cell. This normalization chosen so that the descriptor output of each pair converges at 1 (when created with reasonable values of \(sigma\)). In a similar fashion, each triplet in \(k=3\) is multiplied by \(V/N_{A}N_{B}N_{C}\).

Periodic systems

When applying MBTR to periodic systems, use periodic=True in the constructor. For periodic systems a weighting function needs to be defined, and an exception is raised if it is not given. The weighting essentially determines how many periodic copies of the cell we need to include in the calculation, and without it we would not know when to stop the periodic repetition. The following code demonstrates how to apply MBTR on a periodic crystal:

desc = MBTR(
    species=["H"],
    periodic=True,
    geometry={"function": "inverse_distance"},
    grid={"min": 0, "max": 1.0, "sigma": 0.02, "n": 200},
    weighting={"function": "exp", "scale": 1.0, "threshold": 1e-3},
    sparse=False,
)

a1 = bulk('H', 'fcc', a=2.0)
output = desc.create(a1)

A problem with periodic crystals that is not directly solved by the MBTR formalism is the fact that multiple different cells shapes and sizes can be used for the same crystal. This means that the descriptor is not unique: the same crystal can have multiple representations in the descriptor space. This can be an issue when predicting properties that do not scale with system size, e.g. band gap or formation energy per atom. The following code and plot demonstrates this for different cells representing the same crystal:

a1 = bulk('H', 'fcc', a=2.0)                     # Primitive
a2 = a1*[2, 2, 2]                                # Supercell
a3 = bulk('H', 'fcc', a=2.0, orthorhombic=True)  # Orthorhombic
a4 = bulk('H', 'fcc', a=2.0, cubic=True)         # Conventional cubic

# Without normalization the shape of the output is the same, but the intensity
# is not
desc.normalization = "none"

output = desc.create([a1, a2, a3, a4])
fig, ax = mpl.subplots()
ax.plot(output[0, :], label="Primitive cell")
ax.plot(output[1, :], label="2x2 supercell")
ax.plot(output[2, :], label="Orthorhombic cell")
ax.plot(output[3, :], label="Conventional cubic cell")
ax.legend()
mpl.show()

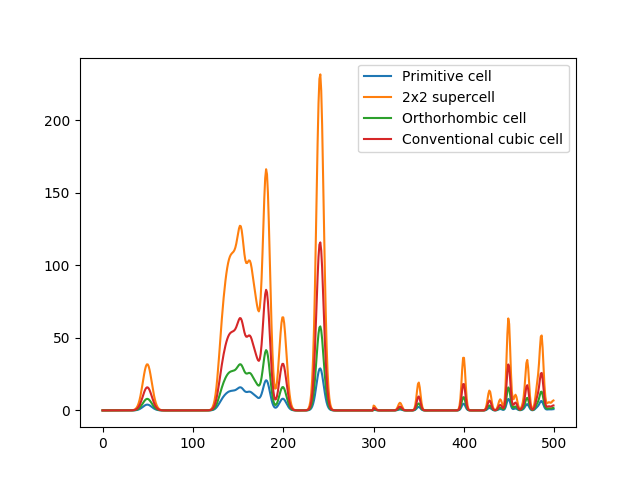
MBTR unnormalized — The raw MBTR output for different cells representing the same crystal. The shapes in the output are the same, but the intensities are different (intensities are integer multiples of the primitive system output)

However, if the output is normalized (see the example about different normalization methods) we can recover truly identical output for the different cells representing the same material:

# With normalization to unit euclidean length the outputs become identical
desc.normalization = "l2"
output = desc.create([a1, a2, a3, a4])
fig, ax = mpl.subplots()
ax.plot(output[0, :], label="Primitive cell")
ax.plot(output[1, :], label="2x2 supercell")
ax.plot(output[2, :], label="Orthorhombic cell")
ax.plot(output[3, :], label="Conventional cubic cell")
ax.legend()
mpl.show()

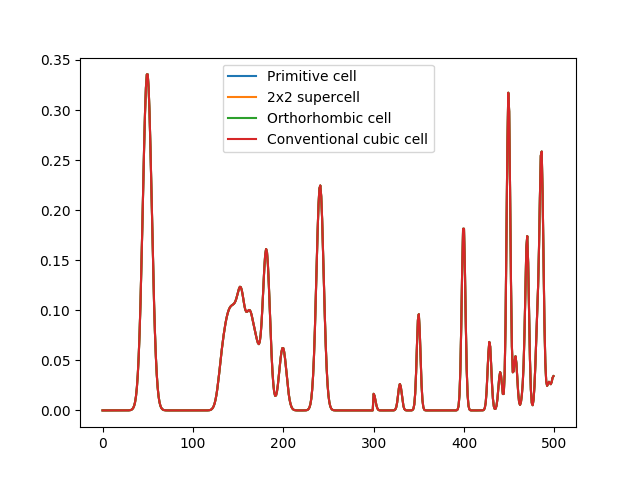
MBTR normalized — The normalized MBTR output for different cells representing the same crystal. After normalising the output with `normalization='l2_each'`, the outputs become identical.

DScribe achieves the completely identical MBTR output for different periodic supercells by taking into account the translational multiplicity of the atomic pairs and triples in the system. This is done in practice by weighting the contribution of the pair and triples by how many different periodic repetitions of the original cell are involved in forming the pair or triple.

[1]

Haoyan Huo and Matthias Rupp. Unified representation of molecules and crystals for machine learning. arXiv e-prints, pages arXiv:1704.06439, Apr 2017. arXiv:1704.06439.