Sine matrix

The sine matrix [1] captures features of interacting atoms in a periodic system with a very low computational cost. The matrix elements are defined by

\[\begin{split}\begin{equation} M_{ij}^\mathrm{sine}=\left\{ \begin{matrix} 0.5 Z_i^{2.4} & \text{for } i = j \\ \frac{Z_i Z_j}{\lvert \mathbf{B} \cdot \sum_{k=\{x,y,z\}} \hat{\mathbf{e}}_k \sin^2 \left( \pi \mathbf{B}^{-1} \cdot \left( \mathbf{R}_{i} - \mathbf{R}_{j} \right) \right)\rvert} & \text{for } i \neq j \end{matrix} \right. \end{equation}\end{split}\]

Here \(\mathbf{B}\) is a matrix formed by the lattice vectors and \(\hat{\mathbf{e}}_k\) are the cartesian unit vectors. This functional form has no physical interpretation, but it captures some of the properties of the Coulomb interaction, such as the periodicity of the crystal lattice and an infinite energy when two atoms overlap.

Setup

Instantiating the object that is used to create Sine matrices can be done as follows:

The constructor takes the following parameters:

SineMatrix.__init__(n_atoms_max, permutation='sorted_l2', sigma=None, seed=None, flatten=True, sparse=False)

Parameters

• n_atoms_max (int) – The maximum nuber of atoms that any of the samples can have. This controls how much zeros need to be padded to the final result.

• permutation (string) –

  Defines the method for handling permutational invariance. Can be one of the following:

  • none: The matrix is returned in the order defined by the Atoms.

  • sorted_l2: The rows and columns are sorted by the L2 norm.

  • eigenspectrum: Only the eigenvalues are returned sorted by their absolute value in descending order.

  • random: The rows and columns are sorted by their L2 norm after applying Gaussian noise to the norms. The standard deviation of the noise is determined by the sigma-parameter.

• sigma (float) – Provide only when using the random-permutation option. Standard deviation of the gaussian distributed noise determining how much the rows and columns of the randomly sorted matrix are scrambled.

• seed (int) – Provide only when using the random-permutation option. A seed to use for drawing samples from a normal distribution.

• flatten (bool) – Whether the output of create() should be flattened to a 1D array.

• sparse (bool) – Whether the output should be a sparse matrix or a dense numpy array.

Creation

After the Sine matrix has been set up, it may be used on periodic atomic structures with the create()-method.

The call syntax for the create-function is as follows:

SineMatrix.create(system, n_jobs=1, verbose=False)

Return the Sine matrix for the given systems.

Parameters

• system (ase.Atoms or list of ase.Atoms) – One or many atomic structures.

• n_jobs (int) – Number of parallel jobs to instantiate. Parallellizes the calculation across samples. Defaults to serial calculation with n_jobs=1.

• verbose (bool) – Controls whether to print the progress of each job into to the console.

Returns

Sine matrix for the given systems. The return type depends on the ‘sparse’ and ‘flatten’-attributes. For flattened output a single numpy array or sparse scipy.csr_matrix is returned. The first dimension is determined by the amount of systems.

Return type

np.ndarray | scipy.sparse.csr_matrix

Note that if you specify in n_atoms_max a lower number than atoms in your structure it will cause an error. The output will in this case be a flattened matrix, specifically a numpy array with size #atoms * #atoms. The number of features may be requested beforehand with the get_number_of_features()-method.

In the case of multiple samples, the creation can also be parallellized by using the n_jobs-parameter. This splits the list of structures into equally sized parts and spaws a separate process to handle each part.

Examples

The following examples demonstrate usage of the descriptor. These examples are also available in dscribe/examples/sinematrix.py.

Interaction in a periodic crystal

The following code calculates the interaction value, as defined by the sine matrix, between two aluminum atoms in an FCC-lattice. The values are calculated in the xy-plane.

This code will result in the following plot:

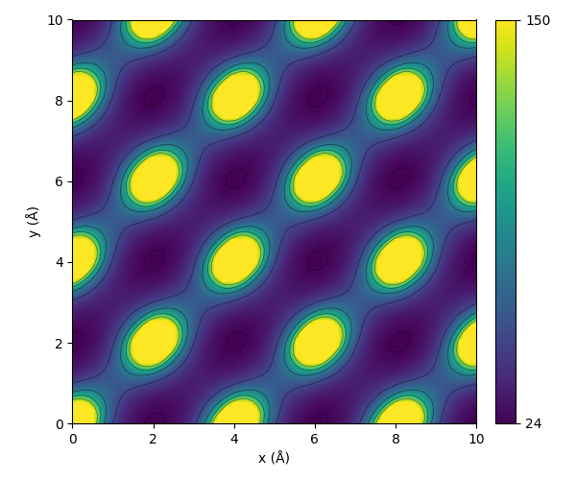
Illustration of the periodic interaction defined by the sine matrix.

From the figure one can see that the sine matrix correctly encodes the periodicity of the lattice. Notice that the shape of the interaction is however not perfectly spherical.

1

Felix Faber, Alexander Lindmaa, O. Anatole von Lilienfeld, and Rickard Armiento. Crystal structure representations for machine learning models of formation energies. International Journal of Quantum Chemistry, 115(16):1094–1101, 8 2015. doi:10.1002/qua.24917.